Aprender con el CUBO DE RUBIK

Aprendamos con el  Cubo de Rubik: para grado sexto de 2012    I. E. Maestro Pedro Nel Gómez,  Barrio Florencia - Medellín

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

Un cubo de Rubik resuelto.

Un cubo de Rubik sin resolver.

El cubo de Rubik (o cubo mágico, como se conoce en algunos países) es un rompecabezas mecánico inventado por el escultor y profesor de arquitectura húngaro Ernö Rubik en 1974.^[1] Se trata de un conocido rompecabezas cuyas caras están divididas en cuadrados de un mismo color que se pueden cambiar de posición. El objetivo de resolver el rompecabezas se consigue al colocar todos los cuadrados de cada cara del cubo con el mismo color.
Se ha estimado que se han vendido más de 350 millones de cubos de Rubik o imitaciones en todo el mundo. Su sencillo mecanismo sorprende tanto desde el punto de vista mecánico, al estudiar su interior, como por la complejidad de las combinaciones que se consiguen al girar sus caras. El cubo celebró su 25º aniversario en 2005 por lo que salió a la venta una edición especial del mismo en la que la cara blanca fue remplazada por una reflejante en la que se leía "Rubik's Cube 1980-2005".
En el cubo típico, cada cara está cubierta por nueve cuadrados de un color sólido. Cuando está resuelto, cada cara es de un mismo color. Sin embargo existen variaciones con otro número de cuadrados por cara. Las principales versiones que hay son las siguientes: el 2×2×2 "Cubo de bolsillo", el 3×3×3 el cubo de Rubik estándar, el 4×4×4 (La venganza de Rubik), el 5×5×5 (El Cubo del Profesor) y desde septiembre de 2008 el 6×6×6 (V-Cube 6) y el 7×7×7 (V-Cube 7) de Verdes Panagiotis.^[2]

Contenido [ocultar] 1 Historia y patentes 2 Descripción 2.1 Número de combinaciones posibles 3 Soluciones 3.1 Soluciones óptimas 4 Competiciones 4.1 Competiciones alternativas 5 Variaciones 5.1 Variaciones extra dimensionales 6 Véase también 7 Referencias 8 Enlaces externos

[editar] Historia y patentes

En marzo de 1970, Larry Nichols inventó un rompecabezas de 2×2×2 (similar a los ya conocidos cubos de Rubik) y lo llamó "Rompecabezas con Piezas Rotables en Grupos". El juguete de Nichols se sostenía usando imanes. Obtuvo una patente canadiense y posteriormente otra estadounidense el 11 de abril de 1972, dos años antes de que Rubik inventara su cubo mejorado.
El 9 de abril de 1970, Frank Fox patentó su "3×3×3 esférico". Recibió una patente del Reino Unido (1344259) el 16 de enero de 1974.
Rubik inventó su "Cubo Mágico" en 1974 y obtuvo una patente Húngara (HU170062) por el Cubo Mágico en 1975, pero no adquirió otras patentes internacionales. Los primeros productos de este invento salieron a la venta en 1977 en jugueterías de Budapest. El cubo mágico se unía por medio de piezas de plástico ensambladas entre sí, las cuales eran más baratas de producir que los imanes de Nichols. En septiembre de 1979 hizo un trato con Ideal Toys para llevar el Cubo Mágico a occidente, y el juguete llegó por primera vez a las jugueterías fuera de Hungría en febrero de 1980.
Después del lanzamiento internacional el éxito del Cubo en las jugueterías occidentales se detuvo brevemente para que el juguete pudiera adecuarse a los estándares occidentales de seguridad y empaquetado. Se produjo un cubo más ligero e Ideal Toys decidió cambiarle el nombre; se consideraron el "El nudo gordiano" y "Oro Inca", pero la compañía finalmente se decidió por "El cubo de Rubik", y la primera entrega fue exportada de Hungría en mayo de 1980. A raíz de la escasez del producto surgieron muchas imitaciones más baratas.
Nichols le asignó su patente a su compañía empleadora, "Moleculon Research Corp.", que demandó a la Ideal Toys Company en 1982. En 1984 la Ideal perdió la demanda por infracción de patentes y apeló. En 1986 la corte de apelaciones confirmó que el Cubo de Rubik de 2×2×2 "Pocket Cube" infringía la patente de Nichols, pero revirtió el juicio sobre el Cubo de Rubik de 3×3×3.^[3]
Aun estando en proceso la solicitud de patente de Rubik, Terutoshi Ishigi, un ingeniero autodidacta y dueño de una forja cerca de Tokio hizo su solicitud de patente por un mecanismo prácticamente idéntico y recibió una patente (JP55-8192) en 1976; la reinvención de Ishigi se considera independiente por lo general.^{[4] [5]}
Rubik solicitó una segunda patente húngara el 28 de octubre de 1980, y solicitó otras patentes. En Estados Unidos se le dio otra el 19 de marzo de 1983 por el Cubo.
Recientemente el inventor griego Panagiotis Verdes patentó un método para crear cubos más allá del 5×5×5 hasta 11×11×11. Sus diseños, que incluyen mecanismos mejorados para los 3×3×3, 4×4×4 y el 5×5×5 son apropiados para el speedcubing. Hasta el 4 de abril de 2008, estos diseños no estaban ampliamente disponibles aunque hay vídeos de prototipos de hasta 7×7×7 y sus soluciones. Se anunció que estos cubos serían lanzados al mercado en septiembre de 2008 a través de la marca "VCube".^[2]

[editar] Descripción

El interior de un cubo de Rubik.

El invento, descendiente de un primer prototipo de sólo dos capas, es un tipo de rompecabezas consistente en un cubo en el que cada una de sus seis caras está dividida en nueve partes, 3×3×3, lo que conforma un total de 26 piezas (sin contar el mecanismo interior) que se articulan entre sí gracias a una pieza interior oculta, en la que se cruzan los 3 ejes de rotación. Se puede observar tres tipos de piezas visibles que no pierden su condición a lo largo de los múltiples movimientos que se realizan. Estas piezas son:

• 6 piezas centrales de cara, definen el color que corresponde a cada cara y mantienen siempre la posición relativa entre ellas, son de un solo color. En el modelo original el color blanco estaba opuesto al amarillo, el rojo al naranja y el verde al azul.
• 12 piezas arista, se encuentran en los bordes y son de dos colores.
• 8 piezas vértice, se encuentran en las esquinas y son de tres colores.

El Cubo revuelto.

Las piezas del primer tipo están fijadas a la pieza central oculta, mediante unos tornillos o remaches y permiten únicamente el giro en sus 360 grados, dando lugar al giro de toda una cara, arrastrando con ello todas las piezas que se encuentran a su alrededor.
Los otros dos tipos no tienen más fijación que su propio diseño, lo que permite que giren alrededor de las primeras de una forma sorprendente.

[editar] Número de combinaciones posibles

Podemos combinar entre sí de cualquier forma todos los vértices del cubo, lo que da lugar a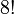 posibilidades. Con las aristas pasa lo mismo; es decir, que podemos combinarlas como se desee, lo que da lugar a posibilidades, pero la permutación total de vértices y aristas debe de ser en total par, lo que nos elimina la mitad de las posibilidades. Por otra parte, podemos rotar todos los vértices como queramos salvo uno sin cambiar nada más en el cubo. La orientación del último vértice vendrá determinada por la que tengan los otros siete, y esto nos crea 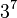posibilidades. Igual debe ocurrir con las aristas, pues aparecen posibilidades más. En total tendremos que el número de permutaciones posibles en el Cubo de Rubik es de: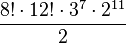
= 43.252.003.274.489.856.000
Es decir, cuarenta y tres trillones doscientos cincuenta y dos mil tres billones doscientos setenta y cuatro mil cuatrocientos ochenta y nueve millones ochocientas cincuenta y seis mil permutaciones.^[6]

[editar] Soluciones

Wikilibros

• Wikilibros alberga un libro o manual sobre Resolver el cubo de Rubik.

Muchas soluciones para el cubo de Rubik se han descubierto de manera independiente. El método más popular fue desarrollado por David Singmaster y publicado en el libro "Notas sobre el Cubo Mágico de Rubik" en 1981. Esta solución consiste en resolver el Cubo capa por capa: a la que se llama Superior, se resuelve primero, seguida de la de en medio, y por último la Inferior. Después de cierta práctica es posible resolver el cubo en menos de 1 minuto. Otros métodos son, por ejemplo, "esquinas primero" y métodos que combinan varios métodos.
Se han desarrollado soluciones rápidas para resolver el cubo lo más rápidamente posible. La solución rápida más común fue desarrollada por Jessica Fridrich. Es un método muy eficiente capa por capa que requiere una mayor cantidad de algoritmos, especialmente para orientar y permutar la última capa. Las esquinas de la primera capa y las aristas de la segunda capa se resuelven simultáneamente, cada esquema se empareja con un borde de la segunda capa. Otra solución bien conocida fue desarrollada por Lars Petrus. En ese método una sección de 2×2×2 se resuelve primero, seguida de otra de 2×2×3, y luego los bordes colocados incorrectamente se resuelven usando un algoritmo de tres movimientos que elimina la necesidad de un posible algoritmo de 32 movimientos. Entre las ventajas de este método es que tiende a dar soluciones en menos movimientos, por esa razón, el método es popular para competencias por número de movimientos.
Las soluciones siguen una serie de pasos e incluyen un conjunto de algoritmos para cada paso. Un algoritmo, también conocido como proceso u operador, es una serie de giros que lleva a cabo un objetivo específico. Por ejemplo, un algoritmo puede intercambiar las posiciones de tres esquinas, dejando el resto de las piezas en su mismo lugar. Las soluciones básicas requieren aprender por lo menos cuatro o cinco algoritmos, pero son por lo general ineficientes, necesitando alrededor de 100 giros para resolver el cubo completo de 3×3×3. En comparación, la solución avanzada de Fridrich requiere aprender 78 algoritmos (algoritmos únicamente para la última capa) pero permite resolver el cubo en un promedio de 55 movimientos. Un tipo diferente de solución es la desarrollada por Ryan Heise, la cual no utiliza algoritmos, sino más bien enseña un grupo de principios fundamentales que se pueden usar para resolver el cubo en menos de 40 movimientos.

[editar] Soluciones óptimas

En 1982 David Singmaster y Alexander Frey plantearon la hipótesis de que el número de movimientos necesarios para resolver el Cubo de Rubik, dado un algoritmo ideal, podría estar "en los veinte más bajos". En 2007, Daniel Kunkle y Gene Cooperman usaron una supercomputadora para demostrar que cualquier cubo de 3×3×3 podía ser resuelto en un máximo de 26 movimientos. ^{[7] [8]} En marzo de 2008, Tomas Rokicki bajó el máximo a 25 movimientos. ^[9] En Julio de 2010 se demostró que cualquier posición del cubo de Rubik puede resolverse en 20 movimientos o menos. Hay muchos algoritmos para resolver el cubo, pero aquellos que puede memorizar un ser humano requieren normalmente más de 40 movimientos. Por ello a la estrategia ideal se le suele llamar "algoritmo de Dios" y el número de movimientos de este algoritmo en la peor situación "número de Dios". Por ejemplo, la posición conocida como "super volteo" (U R2 F B R B2 R U2 L B2 R U' D' R2 F R' L B2 U2 F2), donde cada arista está en su posición correcta pero mal orientada, requiere 20 movimientos para ser resuelta. Fue la primera que se encontró que requería 20 movimientos. ^[10]

[editar] Competiciones

Se han llevado a cabo muchas competiciones en busca de la solución más rápida del Cubo de Rubik. El primer torneo mundial lo organizó Guiness de los récords, y se llevó a cabo en Múnich en 1981. Todos los cubos fueron girados 40 veces y lubricados con vaselina. El ganador oficial, con una marca de 38 segundos fue Jury Froeschl, nacido en Múnich.
El primer torneo mundial internacional se llevó a cabo en Budapest el 5 de junio de 1982, y lo ganó Mihn Thai, un estudiante vietnamita de Los Ángeles con un tiempo de 22.95 segundos. Desde 2003, las competiciones se determinan por el promedio de tiempo (de 5 intentos); pero el mejor tiempo único de todos también lo registra la World Cube Association, que mantiene el registro de las plusmarcas mundiales.^[11]
En 2004 la WCA hizo obligatorio usar un dispositivo especial llamado Cronómetro Stackmat. La actual plusmarca mundial la sustenta el australiano Feliks Zemdegs^[12] con un mejor tiempo de 6.77 segundos. Es probable que mucha gente haya hecho tiempos mejores fuera de las competiciones, pero no son aceptados ya que no puede comprobarse si cumplen con los estándares.

[editar] Competiciones alternativas

También se han hecho competiciones resolviendo el Cubo de maneras inusuales. Estas incluyen:

• Resolverlo con los *ojos vendados^[13]
• Resolverlo con una persona vendada y la otra diciéndole que giros hacer
• Resolverlo con una mano^[14]
• Resolver el cubo bajo el agua en una sola respiración.^[15]
• Resolver el cubo con los pies^[16]

[editar] Variaciones

Variaciones del Cubo de Rubik (de izquierda a derecha) V-Cube 7, La Venganza de Rubik, El cubo del Profesor, El cubo de Rubik, V-Cube 6, y el cubo de Bolsillo.

Existen muchas variaciones del Cubo de Rubik original y también de rompecabezas parecidos, de forma cúbica o de otras distintas. Entre las variaciones cúbicas destaca el "Cubo Mágico" el cual es mecánicamente idéntico al original, pero usa números de colores en sus caras de tal manera que la única forma de resolverlo es que todos los números estén al derecho en la misma cara, adicionalmente los números de las caras forman cuadrados mágicos los cuales pueden tener todos la misma constante. Un cubo muy similar es el cuboku en el cual el objetivo es formar sudokus con los números de las caras. O un cubo cortado de manera no paralela a las caras: el Skewb‎

Un Megaminx de 6 colores resuelto.

Otras incluyen colocar imágenes en lugar de colores o diseños de colores que confundan al que resuelve, como colocar en un 4×4×4 cuatro colores distintos en cada cara para un total de 24 colores distintos. O también reducir el número de colores a 3.
Entre las formas no cúbicas destacan los cubos extendidos que tienen una o más capas adicionales, las cuales pueden ser completa o parcialmente funcionales. También están los rompecabezas basados en mapamundis y otros sólidos platónicos: el Skewb diamante, el Megaminx, el Pyraminx o el Dogic entre otros. Para la mayoría de estas variaciones es posible pensar en otros rompecabezas que estén partidos en un mayor número de piezas de la misma manera que La Venganza de Rubik por ejemplo, así como distintas maneras de colorearlos.

Pyraminx resuelto

Durante el auge del cubo, la empresa de videojuegos Atari lanzó sus cartuchos para consola Atari 2600 llamados "Rubik's Cube" (CX2698), "Atari Video Cube" (reedición que cambió el nombre por razones de copyright, CX2670) y el prototipo "Rubik's Cube 3D" que no salió al mercado.^[17]

[editar] Variaciones extra dimensionales

En 1994 Melinda Green, Don Hatch, y Jay Berkenilt crearon el llamado "MagicCube4D", el cual es un modelo tetradimensional análogo de el Cubo de Rubik en Java el cual consiste en hipercubos desde 2×2×2×2 hasta 5×5×5×5. Con muchos más estados posibles este objeto es mucho más difícil de resolver. Hasta ahora sólo 78 personas lo han conseguido resolver. La forma geométrica de este cubo es de un teseracto, el cual tiene cada línea dividida en 3 partes iguales para el rompecabezas estándar, el resultado de esto es que además de las piezas de 1, 2, y 3 colores del cubo de 3 dimensiones existe un cuarto tipo de pieza con 4 colores cada una, las cuales están en los vértices.
En 2006 Roice Nelson y Charlie Nevill crearon el modelo pentadimensional "Magic Cube 5D" desde 2×2×2×2×2 hasta 5×5×5×5×5 que hasta ahora ha sido resuelto sólo por doce personas. En este rompecabezas existen además piezas con cinco colores las cuales están también sobre los vértices.

[editar] Véase también

• Cubo de bolsillo‎ (2×2×2)
• La venganza de Rubik‎ (4×4×4)
• El Cubo del Profesor (5×5×5)
• V-Cube 6 (6×6×6)
• V-Cube 7 (7×7×7)
• Skewb‎
• Skewb diamante
• Pyraminx
• Megaminx
• Dogic
• Cuboku
• Impossiball

[editar] Referencias

1. ↑ Rubik's Official Online Site
2. ↑ ^{a b} Verdes Panagiotis. [1]
3. ↑ Moleculon Research Corporation v. CBS, Inc.
4. ↑ http://cubeman.org/cchrono.txt
5. ↑ The History of Rubik's Cube - Erno Rubik
6. ↑ rubikaz.com
7. ↑ «Twenty-Six Moves Suffice for Rubik's Cube».
8. ↑ Julie J. Rehmeyer. «Cracking the Cube». MathTrek. Consultado el 09-08-2007.
9. ↑ Tom Rokicki. «Twenty-Five Moves Suffice for Rubik's Cube». Consultado el 24-03-2008.
10. ↑ «God's Number is 20».
11. ↑ «[http://www.worldcubeassociation.org/results/regions.php?regionId=&eventId=333&years=&history=History World Cube Association Official Results]». World Cube Association. Consultado el 16-02-2008.
12. ↑ Récord del mundo
13. ↑ Rubik's 3x3x3 Cube: Blindfolded records
14. ↑ Rubik's 3x3x3 Cube: One-handed
15. ↑ Rubik's Cube 3x3x3: Underwater
16. ↑ Rubik's 3x3x3 Cube: With feet
17. ↑ Atariage.com

[editar] Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre cubo de Rubik. Commons
• El cubo de rubik de la A a la Z: Solución en español a distintos niveles y foro
• Animación paso a paso Explicación en vídeo (castellano)
• Animación paso a paso Explicación en vídeo (inglés)
• Resolución en 20 movimientos

Taller Para padres y alumnos

INSTITUCIÓN EDUCATIVA MAESTRO PEDRO NEL GÒMEZ.

     B. FLORENCIA MEDELLÍN.

  “Forjar Seres Humanos Íntegros.”

TALLER DE PRACTICA PERÍDO 1, 2012.  ÁREA: MATEMÁTICAS GRUPO 6____

ALUMNOS Y PADRES

Estimado padre de familia, aquí encuentra un taller de apoyo para trabajar con sus hijos.

Ejercicios de números naturales

1.Busca el término desconocido e indica su nombre en las siguientes operaciones:

1. 327 + ....... = 1.208

2. ....... – 4.121 = 626

3. 321 · ....... = 32 100

4. 28.035 : ....... = 623 

2.Busca el término desconocido en las siguientes operaciones:

1. 4 · (5 + ...) = 36

2. (30 – ...) : 5 + 4 = 8

3. 18 · ... + 4 · ... = 56

4. 30 – ... : 8 = 25

3.Calcular de dos modos distintos la siguiente operaciones:

1. 17 · 38 + 17 · 12 =

2. 6 · 59 + 4 · 59 =

3.(6 + 12) : 3

4.Sacar factor común:

1. 7 · 5 – 3 · 5 + 16 · 5 – 5 · 4 =

2. 6 · 4 – 4 · 3 + 4 · 9 – 5 · 4 =

3.8 · 34 + 8 · 46 + 8 · 20 =

5.Expresa en forma de potencias:

1. 50 000

2. 3 200

3. 3 000 000

6.Escribe en forma de una sola potencia:

1. 3³ · 3⁴ · 3 =

2. 5⁷ : 5³ =

3. (5³)⁴ =

4. (5 · 2 · 3)⁴ =

5. (3⁴)⁴ =

6. [(5³)⁴ ]² =

7. (8²)³

8. (9³)²

9. 2⁵ · 2⁴ · 2 =

10. 2⁷ : 2⁶ =

11. (2²)⁴ =

12. (4 · 2 · 3)⁴ =

13.(2⁵)⁴ =

14. [(2³ )⁴]⁰=

15. (27²)⁵=

16. (4³)² =

7.Utilizando potencias, haz la descomposición polinómica de estos números:

1. 3 257

2. 10 256

3.125 368

8.Calcular las raíces:

1.

2.

3.

9.Realiza las siguientes operaciones combinadas teniendo en cuenta su prioridad:

1. 27 + 3 · 5 – 16 =

2. 27 + 3 – 45 : 5 + 16 =

3. (2 · 4 + 12) (6 − 4) =

4. 3 · 9 + (6 + 5 – 3) – 12 : 4 =

5. 2 + 5 · (2 · 3)³ =

6. 440 − [30 + 6 (19 − 12)] =

7. 2{4 [7 + 4 (5 · 3 − 9)] − 3 (40 − 8)} =

8. 7 · 3 + [6 + 2 · (2³ : 4 + 3 · 2) – 7 · ] + 9 : 3 =

PROGRAMA CURRICULAR DE SÉXTO 2012

INSTITUCIÓN EDUCATIVA  MAESTRO PEDRO NEL GÓMEZ

    PLAN DE ÁREA DE MATEMÁTICAS

2011

GRADO: __6º                                                                    INTENSIDAD HORARIA: _5__ horas semanales                     PERIODO: _01_____               

DOCENTES:  CARLOS MANUEL PACHECO GONZALEZ   

OBJETIVO DE GRADO: Identificar  el concepto de fracción, sus operaciones y representación grafica en la recta numérica, el análisis de datos estadísticos  por medio de juegos didácticos, juegos de regletas y el geoplano, para lograr en el estudiante el desarrollo de las capacidades cognitivas y el pensamiento lógico matemático resolviendo  problemas de la vida cotidiana y desarrolle  esquemas de pensamiento.               

PENSAMIENTOS MATEMÁTICOS: PENSAMIENTO NUMÉRICO Y SISTEMAS NUMERICOS PENSAMIENTO VARIACIONAL Y SISTEMAS ALGEBRAICOS Y ANALÍTICOS
COMPETENCIAS ·  Usar representaciones concretas y prácticas para explicar el valor posicional en el sistema decimal. ·  Justificar operaciones matemáticas (algoritmos, utilizando relaciones y las propiedades de las operaciones. ·  Utilizar diferentes métodos para solucionar una ecuación sencilla
ESTÁNDARES BÁSICOS DE COMPETENCIA PENSAMIENTO NUMÉRICO Y SISTEMAS NUMERICOS ·  Formulo y resuelvo problemas aplicando conceptos de la teoría de números (números primos, múltiplos) en contextos reales y matemáticos. ·  Resuelvo y formulo problemas utilizando propiedades fundamentales de la teoría de números ·         Justifico operaciones aritméticas utilizando relaciones y las propiedades de las operaciones. PENSAMIENTO VARIACIONAL Y SISTEMAS ALGERAICOS Y ANALITICOS ·         Reconozco el conjunto de valores de una variable en situaciones concretas de cambio(variación) ·         Utilizo métodos informales(ensayo-error, complementación) en la  solución de ecuaciones
SITUACIÓN PROBLEMA	CONTENIDOS			INDICADORES DE DESEMPEÑO
	Conocimientos  conceptuales	Conocimientos  procedimentales	Conocimientos actitudinales
“Los números naturales” La invención de los números naturales, ha sido para el hombre uno de los grandes triunfos en la historia de las matemáticas, el estudiante empieza a establecer relaciones de bastante, poco, grande, pequeño, de manera intrínseca establece el orden, y le asigna un número (cardinal) a un número exacto de objetos o sucesos.	Construcción del conjunto de los números naturales Proposiciones y el valor de verdad de un enunciado. Reconocimiento de las operaciones básicas y sus propiedades en los números naturales. Definición de número natural y su representación en la recta numérica. Concepto de ecuación de primer grado con una incógnita y planteamiento de problemas que conlleven a la solución de ésta.	Construcción de los números naturales en el sistema decimal. Aplicación de la estructura aditiva y multiplicativa en el sistema de los números naturales. Resolución de ecuaciones de primer grado con una incógnita, partiendo de relaciones de orden y de cardinalidad en los números naturales. Representación de las operaciones suma y resta en la recta numérica con los números naturales. Utilización de los diferentes métodos para establecer si un número es divisible por 2, 3, 5, 7 y 10.	Curiosidad e interés para investigar sobre la aplicabilidad de las operaciones básicas en los números naturales. Valoración de la importancia de los números naturales en el sistema decimal. Sentido crítico ante la solución de problemas de una o dos operaciones básicas. Valorar la importancia del lenguaje lógico matemático en la solución de ecuaciones. Valorar la importancia del trabajo en equipo, como manera efectiva de solucionar problemas matemáticos en un grado alto de complejidad.	Utilizar diferentes estrategias de conteo para establecer las operaciones entre conjuntos como unión, intersección, diferencia, diferencia simétrica. Resuelve y formula problemas a partir de las interrelaciones entre conjuntos. Aplica estrategias para resolver algoritmos relacionados con las propiedades de la suma y multiplicación en los números naturales.. Resuelve diversos problemas de la vida cotidiana utilizando los números naturales relacionados con ecuaciones.
Preguntas Orientadoras ¿ Cuáles son las relaciones que se establecen entre los números, para determinar cuándo un número es primo o compuesto?. ¿Cuáles son los procesos que  deben desarrollar los estudiantes para obtener un buen cálculo mental.

INSTITUCIÓN EDUCATIVA  MAESTRO PEDRO NEL GÓMEZ

    PLAN DE ÁREA DE MATEMÁTICAS

2011

GRADO: __6º                                                                    INTENSIDAD HORARIA: _5__ horas semanales                     PERIODO: _02_____               

DOCENTES:  CARLOS MANUEL PACHECO GONZALEZ                  

OBJETIVO DE GRADO: Identificar  el concepto de fracción, sus operaciones y representación grafica en la recta numérica, el análisis de datos estadísticos  por medio de juegos didácticos, juegos de regletas y el geoplano, para lograr en el estudiante el desarrollo de las capacidades cognitivas y el pensamiento lógico matemático resolviendo  problemas de la vida cotidiana y desarrolle  esquemas de pensamiento.               

PENSAMIENTOS MATEMÁTICOS: PENSAMIENTO VARIACIONAL Y SISTEMAS ALGEBRAICOS Y ANALITICOS PENSAMIENTO NUMÉRICO Y SISTEMAS NUMÉRICOS
COMPETENCIAS ·  Establecer las relaciones entre los números enteros y los números racionales. ·  Resolver algoritmos del mínimo común múltiplo (mcm) y Máximo Común Divisor (MCD). ·  Resolver y formular problemas de números fraccionarios aplicando las operaciones de suma y resta. ·  Presenta argumentos que verifiquen y validen los procedimientos necesarios, para resolver situaciones problema de la vida cotidiana con los números fraccionarios.
ESTÁNDARES BÁSICOS DE COMPETENCIA PENSAMIENTO VARIACINAL Y SISTEMAS ALGEBRAICOS Y ANALITICOS ·         Utilizo métodos informales(ensayo-error, complementación) en la solución de ecuaciones PENSMIENTO NUMÉRICO Y SISTEMAS NUMERICOS. ·         Resuelvo y formulo problemas cuya solución requiere de la potenciación y la radicación. ·         Justifico la representación polinomial de números racionales, utilizando las propiedades del sistema decimal. ·         Utilizo números (fracciones decimales, razones, porcentajes) para resolver problemas en contextos de medida.
SITUACIÓN PROBLEMA	CONTENIDOS			INDICADORES DE DESEMPEÑO
	Conocimientos  conceptuales	Conocimientos  procedimentales	Conocimientos actitudinales
“Explorando los  números enteros fraccionarios” Los números fraccionarios siempre han generado un malestar entre los estudiantes que inician la Secundaria, considerar un todo en partes iguales, requiere de un grado de pensamiento superior, el niño requiere mayor esfuerzo, estas operaciones se asocian al concepto de división, operación básica que constituye uno de los mayores retos o procesos de asimilación que el niño aprende, no se sabe si la diferencia radica, en que la operación con el número fraccionario requiere de una asociación exhaustiva de la suma, resta, multiplicación y la división, y ello requiere de un tipo de pensamiento más refinado.	Conceptualización de número fraccionario y su representación gráfica en la recta numérica. Aplicación de las cuatro operaciones básicas a través de un algoritmo. Utilización de las cuatro operaciones básicas para resolver problemas de fraccionarios. Solución de problemas con los números decimales. Solución de ejercicios con signos de agrupación, utilizando los números Enteros como eje principal. Potenciación y radicación con fraccionarios	Exploración del material didáctico con las tortas fraccionarias para la comprensión de un todo en partes iguales. Aplicación de estructura aditiva y multiplicativa en el sistema de los números faccionarios. Utilización del número fraccionario para representar o aplicarlos a problemas del entorno. Resolución de problemas con los números fraccionarios. Utilización del juego con regletas y tortas fraccionarias, para ayudar al niño en la asimilación del concepto de número fraccionario.	Curiosidad e interés por investigar y aprender sobre el número fraccionario y los números decimales. Valoración del material didáctico para solucionar problemas. Reconocimiento y valoración del trabajo en equipo, como manera eficaz para perfeccionar los conocimientos dados por el profesor. Sentido crítico ante soluciones intuitivas, ya sea por parte del alumno o del profesor. Valorar la importancia de una buena disciplina dentro del aula a la hora de la explicación por parte del profesor.	Establece relaciones entre los números fraccionarios que generan patrones de formación, a la hora de dar solución a un problema. Utiliza el lenguaje matemático del número fraccionario, para representar ecuaciones a través de situaciones problema.
Preguntas Orientadoras ¿Qué relaciones se pueden establecer entre los números naturales, los Enteros y los Fraccionarios? ¿Cuáles son los pasos más eficientes para resolver un algoritmo o un problema de números fraccionarios? ¿Cómo grafico en la recta numérica una amplificación o una simplificación de números fraccionario

INSTITUCIÓN EDUCATIVA  MAESTRO PEDRO NEL GÓMEZ

    PLAN DE ÁREA DE MATEMÁTICAS

2011

GRADO: __6º                                                                    INTENSIDAD HORARIA: _5__ horas semanales                     PERIODO: _03_____               

DOCENTES:  CARLOS MANUEL PACHECO GONZÁLEZ   

OBJETIVO DE GRADO: Identificar  el concepto de fracción, sus operaciones y representación grafica en la recta numérica, el análisis de datos estadísticos  por medio de juegos didácticos, juegos de regletas y el geoplano, para lograr en el estudiante el desarrollo de las capacidades cognitivas y el pensamiento lógico matemático resolviendo  problemas de la vida cotidiana y desarrolle  esquemas de pensamiento.               

PENSAMIENTOS MATEMÁTICOS: PENSAMIENTO MÉTRICO Y SISTEMAS DE MEDIDAS PENSAMIENTO ESPACIAL Y SISTEMAS GEOMÉTRICOS PENSAMIENTO NUMÉRICO Y SISTEMAS NUMERICOS
COMPETENCIAS ·  Establecer las relaciones que existen entre las unidades de longitud, unidades de área y de volumen. ·  Resolver y formular problemas longitud, área y volumen a partir de datos provenientes de las figuras geométricas del entrono. ·  Presentar  en forma organizada procedimientos utilizados al realizar situaciones de aprendizaje a partir de observaciones realizadas con las figuras geométricas del entrono. ·  Argumentar la construcción de superficies a través de unidades lineales y la construcción de figuras en volumen a través de superficies.
ESTÁNDARES BÁSICOS DE COMPETENCIA PENSAMIENTO ESPACIAL Y SISTEMAS GEOMÉTRICOS ·  Represento objetos tridimensionales  desde diferentes posiciones y vistas ·  Clasifico polígonos en  relación con sus propiedades ·  Resuelvo y formulo problemas que involucren relaciones y propiedades de semejanza y congruencia usando representaciones visuales PENSAMIENTO METRICO Y SISTEMAS METRICOS ·  Generalizo procedimientos de cálculo válidos para encontrar el área de regiones planas y el volumen de sólidos. ·  Utilizo técnicas y herramientas para la construcción de figuras planas y cuerpos con medidas dadas ·  Calculo áreas y volúmenes a través de la composición y descomposición de figuras y cuerpos PENSAMIENTO NUMERICO Y SISTEMAS NUMERICOS ·         Resuelvo y formulo problemas utilizando las propiedades fundamentales de la teoría de números ·         Justifico operaciones aritméticas utilizando las relaciones y propiedades de las operaciones
SITUACIÓN PROBLEMA	CONTENIDOS			INDICADORES DE DESEMPEÑO
	Conocimientos  conceptuales	Conocimientos  procedimentales	Conocimientos actitudinales
“Polígonos y poliedros” Es evidente en la escuela Primaria y Secundaria que el niño o joven sale del bachillerato, con pocas bases conceptuales geométricas, el niño sólo conoce algunas figuras geométricas, les sabe hallar su perímetro y hasta su área, pero no tiene la profundidad que se necesita en estas etapas de desarrollo cognitivo que el niño necesita, el joven debe saber construir estas figuras geométricas con regla y compás y hacer estas construcciones en  volumen y luego debe apoyarse en el doblado de papel para construir figuras como el dodecaedro, el cubo y otras figuras más, que le ayudarán primero a comprender el concepto de mostración  y luego el de demostración, la cual la hace más rigurosa. El problema radica en que el educador deja esta área para los últimos quince o veinte días del año lectivo, o por desconocimiento del área.	Conceptualización de los elementos de los poliedros. Relaciones entre polígonos y poliedros. Conceptos de los elementos de las figuras geométricas como perímetro, frontera, apotema, arista, vértice entre otros. Clasificación de las figuras geométricas. Conceptos de: perímetro, área y volumen. Operaciones de unión, intersección y diferencia entre figuras geométricas.	Construcción con regla y compás de las figuras geométricas. Construcción de algunas figuras geométricas en volumen mediante el doblado de papel (origami), con papel reciclable. Medición de diferentes magnitudes (perímetro, área y volumen) Utilización de terminología adecuada para describir los elementos de los poliedros. Resolución de problemas de la geometría a partir  de las relaciones que se establecen entre  los elementos de las figuras geométricas.	Interés por investigar y consultar sobre la construcción de las figuras geométricas. Valoración del material didáctico para solucionar problemas. Sentido crítico ante las soluciones intuitivas. Valorar la importancia y la utilidad del lenguaje matemático. Valoración del trabajo en equipo como apoyo cognitivo para realizar tareas de mayor complejidad.	Utiliza diferentes estrategias de conteo para determinar el número de elementos de los polígonos y poliedros como arista, vértice, ángulo, etc. Utiliza correctamente la regla y compás para construcción de figuras. Aplica el concepto de medida para la construcción de polígonos. Resuelve problemas a partir de un conjunto de datos.

                                              

                    INSTITUCIÓN EDUCATIVA MAESTRO PEDRO NEL GÓMEZ  

    PLAN DE ÁREA DE MATEMÁTICAS

2011

GRADO: __6º                                                                    INTENSIDAD HORARIA: _5__ horas semanales                     PERIODO: _04_____               

DOCENTES:  CARLOS MANUEL PACHECO GONZALEZ                  

OBJETIVO DE GRADO: Identificar  el concepto de fracción, sus operaciones y representación grafica en la recta numérica, el análisis de datos estadísticos  por medio de juegos didácticos, juegos de regletas y el geoplano, para lograr en el estudiante el desarrollo de las capacidades cognitivas y el pensamiento lógico matemático resolviendo  problemas de la vida cotidiana y desarrolle  esquemas de pensamiento.               

PENSAMIENTOS MATEMÁTICOS: PENSAMIENTO VARIACIONAL Y SISTEMAS ALGEBRICOS Y ANALITICOS PENSAMIENTO ALEATORIO Y SISTEMAS DE DATOS PENSAMIENTO NUMÉRICO Y SISTEMAS NUMERICOS
COMPETENCIAS ·  Describir y representar situaciones de variación relacionando diferentes representaciones como (diagramas, expresiones verbales generalizadas y tablas de datos. ·  Reconocer el conjunto de valores de una variable en situaciones concretas. ·  Reconocer la relación entre un conjunto de datos y su representación. ·  Usar representaciones gráficas adecuadas, para presentar diversos tipos de datos como diagramas de barras, diagramas circulares, hacer conjeturas acerca del resultado de un experimento aleatorio, usando proporcionalidad y nociones básicas de probabilidad. ·  Usar medidas de tendencia central como (mediana, moda) para interpretar el comportamiento de un conjunto de variables o de datos.
ESTÁNDARES BÁSICOS DE COMPETENCIA PENSAMIENTO VARIACIONAL Y SISTEMAS ALGEBRAICOS Y ANALITICOS ·         Identifico las características de diversas gráficas cartesianas (de puntos, continuas, formada por segmentos, etc.), en relación con la situación que representa. ·         Analizo las propiedades de variación lineal e inversa en contextos aritméticos y geométricos. ·           PENSAMIENTO  ALEATORIO Y SISTEMAS DE DATOS ·         Predigo y justifico razonamientos y conclusiones usando información estadística ·         Comparo e interpreto datos provenientes de diversas fuentes (prensa, revistas, televisión, experimentos, consultas, entrevistas). PENSAMIENTO NUMERICO Y SISEMAS NUMERICOS ·         Utilizo argumentos combinatorios(tablas, diagramas, listas) como herramienta para la interpretación de situaciones diversas de conteo
SITUACIÓN PROBLEMA	CONTENIDOS			INDICADORES DE DESEMPEÑO
	Conocimientos  conceptuales	Conocimientos  procedimentales	Conocimientos actitudinales
Actualmente se observa como la televisión, prensa, radio, se han convertido en un medio difusor de de la información para el estudiante, pero al mismo tiempo se observa la dificultad de éste para registrar, analizar, conjeturar y predecir el registro de esa información, al estudiante se le dificulta la interpretación de datos estadísticos, la lectura del diagrama de barras, éstas representan para el educando  un lenguaje matemático difícil de interpretar.	Conceptualización de los elementos de los daos estadísticos. Relaciones entre moda, mediana, Frecuencia Absoluta, Frecuencia Relativa, media aritmética. Concepto de Moda, Mediana, Frecuencia Absoluta, Frecuencia Relativa, Media Aritmética. Conceptos de: proporción, Población, Muestra. Concepto de Variable, gráfica de puntos, Gráfica de Barras.	Construcción de graficas con los datos o variables dadas. Formulación de interrogantes ante las gráficas. Resolución de datos para hacerle el análisis. Resolución de problemas de variables. Aplicación de estructuras aditivas y multiplicativas en el sistema de los números reales positivos. Resolución de problemas relacionados con la estadística.	Valoración de los conceptos en la interpretación de tablas de datos. Curiosidad e interés por investigar más sobre estadística. Sentido crítico ante el desarrollo de las gráficas. Valora la utilidad del lenguaje estadístico para el lenguaje matemático. Valoración del trabajo n equipo para reforzarlos conceptos vistos en clase. Saca conclusiones de las gráficas y las compara con la realidad.	Establece relaciones existentes  la Moda, la Mediana, Frecuencia Absoluta, Frecuencia Relativa, Media Aritmética. Resuelve y formula problemas a partir de un conjunto de datos proveniente de observaciones y exploraciones de los sucesos que se repiten o son frecuentes. Aplica el concepto para la interpretación de gráficas. Utiliza el lenguaje matemático apropiado para describir relaciones entre los elementos de  las medidas de tendencia central.
Preguntas Orientadoras ¿Cómo acceder e interpretar el lenguaje matemático intrínseco en los diagramas de barras y tortas fraccionarias para contribuir a un buen desarrollo del pensamiento lógico matemático? ¿Cómo graficar e interpretar eventos frecuentes que rodean el ambiente cotidiano de la escuela?